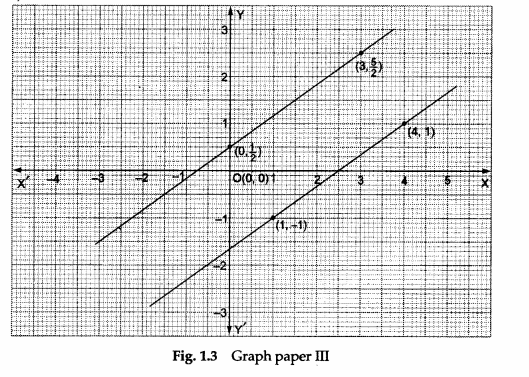
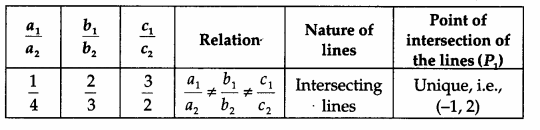
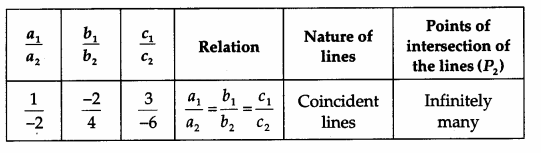
Arithmetic Progression

 

Arithmetic Progression I

Objective
To verify that the given sequence is an arithmetic progression by paper cutting and pasting method

Prerequisite Knowledge
Understanding the concept of an arithmetic progression.

Arithmetic Progression:
A sequence is known as an arithmetic progression (sequence) if the difference between the term and its predecessor always remains constant.

Materials Required
Coloured papers, a pair of scissors, fevicol, geometry box, sketch pens, drawing sheets.

Procedure

1.  Take a given sequence of numbers say A1, A2,  A,…
2.  Cut a rectangular strip from coloured paper of width 1 cm and length A, cm.
3. Repeat the procedure by cutting rectangular strips of same width 1 cm and lengths A,, A3…cm.
4.  Take a graph paper and paste these rectangular strips adjacent to each other in order on graph paper.

[A] Consider a sequence 1, 4, 7, 10, 13.

1.  Take different colour strips of lengths 1 cm, 4 cm, 7 cm, 10 cm, 13 cm and all of the same width 1 cm
   (say).
2.  Arrange and paste these strips in order on a graph paper as shown in fig. (i).

[B] Consider a sequence 1, 4, 8, 10, 11.

1.  Take different colour strips of lengths 1 cm, 4 cm, 8 cm, 10 cm, 11 cm and all of the same width 1 cm (say).
2.  Arrange and paste these strips in order on a graph paper as shown in fig. (ii).

Observation
We observe from fig(i) that the adjoining strips have a common difference in heights i.e. 3 cm and a ladder is formed in which the adjoining steps are constant. Hence it is an arithmetic progression.
In fig (ii) the adjoining strips don’t have a common difference in heights and thus the adjoining steps of ladder are not constant. Hence it is not an arithmetic progression.

Result
Sequence [A] is an AP because common difference between the term and its predecessor remains constant.
Sequence [B] is not an AP because common difference between the term and its predecessor does not remain constant.

Midpoint Theorem

 

Midpoint Theorem

OBJECTIVE

To verify the midpoint theorem

Materials Required

1. A piece of cardboard
2. Two sheets of white paper
3. A geometry box
4. Black color

Theory
Midpoint theorem: The line segment joining the midpoints of any two sides of a triangle is parallel to the third side.

Procedure
Step 1: Paste one of the white sheets on the cardboard.
Draw a  ΔABC on this paper.
Step 2: Mark the midpoints D and E of the sides AB and AC respectively. Join D and E. Colour the ΔADE black.
Step 3: Cut another triangle CEF from the other white sheet so that the ΔCEF is congruent to the ΔADR Colour the ΔCEF also black. Place the ΔCEF on the previous paper as shown in Figure 7.1.

Observations

1. Since ΔCEF is congruent to ΔADE, therefore DE = EF.
   1. Measure DE and BC. We find that DE = ½ BC.
   2. From (i) and (ii), we derive that DF = BC.
2. Since ΔCEF is congruent to ΔADE, therefore AD = FC.
   1. Since D is the midpoint of AB, we have AD = DB.
   2. From (i) and (ii), we get FC = DB.
3. From the above observations, it is clear that DFCB is a parallelogram. Hence, DE||BC.

Result
The midpoint theorem is verified.

Areas of two Similar Triangle

Ratio of the Areas of two Similar Triangle

OBJECTIVE

To verify that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides

Materials Required

1. A piece of cardboard
2. A sheet of white paper
3. A geometry box
4. A tube of glue

Theory
If two triangles ABC and DEF are similar then area of ΔDEF

Procedure
Step 1: Paste the white sheet on the cardboard.
Step 2: Draw a ΔABC on the paper. Now, divide the side AB into four equal parts and label these points P1, P2 and P3 as shown in Figure 8.2. Similarly, divide the side AC into four equal parts and label these points Q1, Q2 and Q3 as shown in Figure 8.2. Also, divide the side BC into equal parts and label these points R1, R2 and R3 as shown in Figure 8.2.
Step 3: Join these points to form the line segments P1Q1, P2Q2 and P3Q3 parallel to the side BC, the line segments Q1R1, Q2R2 and Q3R3 parallel to the side AB, and also the line segments P3R1, P2R2 and P1R3 parallel to the side AC. Thus, the ΔABC is divided into 16 smaller triangles (see Figure 8.2).

Step 4: Draw another triangle DEF having sides DE = ¾ AB, DF = ¾ AC and EF = ¾ BC. Then, clearly the ΔDEF will be similar to the ΔABC.
Step 5: Divide the side DE into three equal parts and label these points X1 and X2 as shown in Figure 8.3.
Divide the side DF into three equal parts and label these points Y1 and Y2 as shown in Figure 8.3.
Also, divide the side EE into three equal parts and label these points Z1 and Z2 as shown in Figure 8.3.
Step 6: Join these points to form the line segments X1Y1 and X2Y2 parallel to the side EE, the line segments Y1Z1 and Y2Z2 parallel to the side DE, and also the line segments X1Z2 and X2Z1 parallel to the side DF. Thus, the ΔDEE is divided into 9 smaller triangles (see Figure 8.3).

Observations

1. ΔABC and ΔDEF are similar to each other.
2. ΔABC is divided into 16 smaller triangles, all congruent to each other. Therefore, all these 16 triangles are equal in area.
3. ΔDEF is divided into 9 smaller triangles, all congruent to each other. Therefore, all these 9 triangles are equal in area.
4. Each small triangle within the ΔABC is congruent to each small triangle within the ΔDEF. Therefore, all these 25 triangles are equal in area (say, equal to M).

Calculations

Result
It is verified that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.

Remarks:
The above result can also be proved for

1. other pairs of corresponding sides of the two triangles.
2. other triangles by dividing each side of a triangle into 3, 4,5 or 6 or even more parts and forming small triangles, and then taking a part of this triangle as a similar triangle.

cbse class10 Lab Work: Pythagoras Theorem

 

Pythagoras Theorem

Objective
To verify Pythagoras theorem by performing an activity.
The area of the square constructed on the hypotenuse of a right-angled triangle is equal to the sum of the areas of squares constructed on the other two sides of a right-angled triangle.

Prerequisite Knowledge

In a right-angled triangle the square of hypotenuse is equal to the sum of squares on the other two sides.

1. Concept of a right-angled triangle.
2. Area of square = (side)2
3. Construction of perpendicular lines.

Materials Required
Coloured papers, pair of scissors, fevicol, geometry box, sketch pens, light coloured square sheet.

Procedure

1.  Take a coloured paper, draw and cut a right-angled triangle ACB right-angled at C, of sides 3 cm, 4 cm and 5 cm as shown in fig. (i).
   
2. Paste this triangle on white sheet of paper.
3. Draw squares on each side of the triangle on side AB, BC and AC and name them accordingly as shown in fig. (ii).
   
4. Extend the sides FB and GA of the square ABFG which meets ED at P and CI at Q respectively, as shown in fig. (iii).
   
5. Draw perpendicular RP on BP which meets CD at R. Mark the parts 1, 2, 3, 4 and 5 of the squares BCDE and ACIH and colour them with five different colours as shown in fig. (iv).
   
6. Cut the pieces 1, 2, 3, 4 and 5 from the squares BCDE and ACIH and place the pieces on the square ABFG as shown in fig. (v).
   

Observation
Cut pieces of squares ACIH and BCDH and completely cover the square ABFG.
∴ Area of square ACIH = AC2 = 9cm2
Area of square BCDE = BC2 = 16cm2
Area of square ABFG = AB2 = 25 cm2
∴ AB2 = BC2 + AC2
25 = 9 + 16

Result
Pythagoras theorem is verified.

__________________________________________________________

Learning Outcome
Students will learn practically that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Activity Time
1. The area of an equilateral triangle described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of equilateral triangles described on the other two sides.

In ∆ACD, AC = DC = DA = 5cm
ar(∆ACD) =  (5)2

In ∆ABE, AB = BE = EA = 3cm
ar(∆ABE) =  (3)2

In ∆BCF, BC = CF = FB = 4cm
ar(∆BCF) = (4)2

Now, ar(∆ABE) + ar(∆BCF) =  (3)2 +  (4)2
=  [9+16]
= [25]
=  (5)2
∴ ar(∆ABE) + ar(∆BCF) = ar(∆ACD) verified.
2. The area of a semi-circle described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of semicircles described on the other two sides of right-angled triangle.

Basic Proportionality Theorem for a Triangle

Basic Proportionality Theorem for a Triangle

Objective
To verify the basic proportionality theorem by using parallel lines board, triangle cut outs.

Basic Proportionality Theorem
If a line is drawn parallel to one side of a triangle, to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

Prerequisite Knowledge

1. Statement of Basic Proportionality theorem.
2. Drawing a line parallel to a given line which passes through a given point.

Materials Required
White chart paper, coloured papers, geometry box, sketch pens, fevicol, a pair of scissors, ruled paper sheet (or Parallel line board).

Procedure

1. Cut an acute-angled triangle say ABC from a coloured paper.
2. Paste the ΔABC on ruled sheet such that the base of the triangle coincides with ruled line.
   
3. Mark two points P and Q on AB and AC such that PQ || BC.
   
4. Using a ruler measure the length of AP, PB, AQ and QC.
5. Repeat the same for right-angled triangle and obtuse-angled triangle.
6. Now complete the following observation table.

Observation

Result
In each set of triangles, we verified that 

Learning Outcome
In all the three triangles the Basic Proportionality theorem is verified.

CBSE Class 10 Mathematics: LAB Works Sample-1: The System of linear Equations

The System of Linear Equations

OBJECTIVE

To use the graphical method to obtain the conditions of consistency and hence to solve a given system of linear equations in two variables

Materials Required

1. Three sheets of graph paper
2. A ruler
3. A pencil

Theory
The lines corresponding to each of the equations given in a system of linear equations are drawn on a graph paper. Now,

1. if the two lines intersect at a point then the system is consistent and has a unique solution.
2. if the two lines are coincident then the system is consistent and has infinitely many solutions.
3. if the two lines are parallel to each other then the system is inconsistent and has no solution.

Procedure
We shall consider a pair of linear equations in two variables of the type
a1x +b1y = c1
a2x +b2y = c2
Step 1: Let the first system of linear equations be
x + 2y = 3 … (i)
4x + 3y = 2 … (ii)
Step 2: From equation (i), we have
y= ½(3 – x).
Find the values of y for two different values of x as shown below.

x	1	3
y	1	0

Similarly, from equation (ii), we have
y=1/3( 2 – 4x).
Then

x	-1	2
y	2	-2

Step 3: Draw a line representing the equation x+2y = 3 on graph paper I by plotting the points (1,1) and (3,0), and joining them.
Similarly, draw a line representing the equation 4x + 3y = 2 by plotting the points (-1, 2) and (2, -2), and joining them.

Step 4: Record your observations in the first observation table.
Step 5: Consider a second system of linear equations:
x – 2y = 3 … (iii)
-2x + 4y = -6 … (iv)
Step 6: From equation (iii), we get

x	3	1
y	0	-l

From equation (iv), we get

x	-3	-1
y	-3	-2

Draw lines on graph paper II using these points and record your observations in the second observation table.

Step 7: Consider a third system of linear equations:
2x – 3y = 5 …(v)
-4x + 6y = 3 … (vi)
Step 8: From equation (v), we get

x	1	4
y	-1	1

From equation (vi), we get

x	0	3
y	½	5/2

Draw lines on graph paper III using these points and record your observations in the third observation table.

Observations
I. For the first system of equations

II. For the second system of equations

III. For the third system of equations

Conclusions

1. The first system of equations is represented by intersecting lines, which shows that the system is consistent and has a unique solution, i.e., x = -1, y = 2 (see the first observation table).
2. The second system of equations is represented by coincident lines, which shows that the system is consistent and has infinitely many solutions (see the second observation table).
3. The third system of equations is represented by parallel lines, which shows that the system is inconsistent and has no solution (see the third observation table).

Remarks: The teacher must provide the students with additional problems for practice of each of the three types of systems of equations.