Midpoint Theorem

 

Midpoint Theorem

OBJECTIVE

To verify the midpoint theorem

Materials Required

1. A piece of cardboard
2. Two sheets of white paper
3. A geometry box
4. Black color

Theory
Midpoint theorem: The line segment joining the midpoints of any two sides of a triangle is parallel to the third side.

Procedure
Step 1: Paste one of the white sheets on the cardboard.
Draw a  ΔABC on this paper.
Step 2: Mark the midpoints D and E of the sides AB and AC respectively. Join D and E. Colour the ΔADE black.
Step 3: Cut another triangle CEF from the other white sheet so that the ΔCEF is congruent to the ΔADR Colour the ΔCEF also black. Place the ΔCEF on the previous paper as shown in Figure 7.1.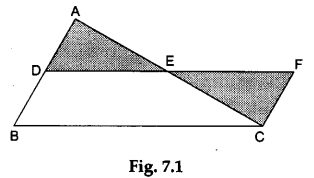

Observations

1. Since ΔCEF is congruent to ΔADE, therefore DE = EF.
   1. Measure DE and BC. We find that DE = ½ BC.
   2. From (i) and (ii), we derive that DF = BC.
2. Since ΔCEF is congruent to ΔADE, therefore AD = FC.
   1. Since D is the midpoint of AB, we have AD = DB.
   2. From (i) and (ii), we get FC = DB.
3. From the above observations, it is clear that DFCB is a parallelogram. Hence, DE||BC.

Result
The midpoint theorem is verified.