The System of Linear Equations
OBJECTIVE
To use the graphical method to obtain the conditions of consistency and hence to solve a given system of linear equations in two variables
Materials Required
- Three sheets of graph paper
- A ruler
- A pencil
Theory
The lines corresponding to each of the equations given in a system of linear equations are drawn on a graph paper. Now,
- if the two lines intersect at a point then the system is consistent and has a unique solution.
- if the two lines are coincident then the system is consistent and has infinitely many solutions.
- if the two lines are parallel to each other then the system is inconsistent and has no solution.
Procedure
We shall consider a pair of linear equations in two variables of the type
a1x +b1y = c1
a2x +b2y = c2
Step 1: Let the first system of linear equations be
x + 2y = 3 … (i)
4x + 3y = 2 … (ii)
Step 2: From equation (i), we have
y= ½(3 – x).
Find the values of y for two different values of x as shown below.
| x | 1 | 3 |
| y | 1 | 0 |
Similarly, from equation (ii), we have
y=1/3( 2 – 4x).
Then
| x | -1 | 2 |
| y | 2 | -2 |
Step 3: Draw a line representing the equation x+2y = 3 on graph paper I by plotting the points (1,1) and (3,0), and joining them.
Similarly, draw a line representing the equation 4x + 3y = 2 by plotting the points (-1, 2) and (2, -2), and joining them.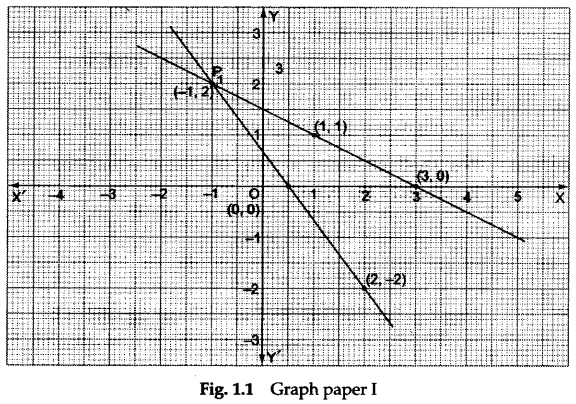
Step 4: Record your observations in the first observation table.
Step 5: Consider a second system of linear equations:
x – 2y = 3 … (iii)
-2x + 4y = -6 … (iv)
Step 6: From equation (iii), we get
| x | 3 | 1 |
| y | 0 | -l |
From equation (iv), we get
| x | -3 | -1 |
| y | -3 | -2 |
Draw lines on graph paper II using these points and record your observations in the second observation table.
Step 7: Consider a third system of linear equations:
2x – 3y = 5 …(v)
-4x + 6y = 3 … (vi)
Step 8: From equation (v), we get
| x | 1 | 4 |
| y | -1 | 1 |
From equation (vi), we get
| x | 0 | 3 |
| y | ½ | 5/2 |
Draw lines on graph paper III using these points and record your observations in the third observation table.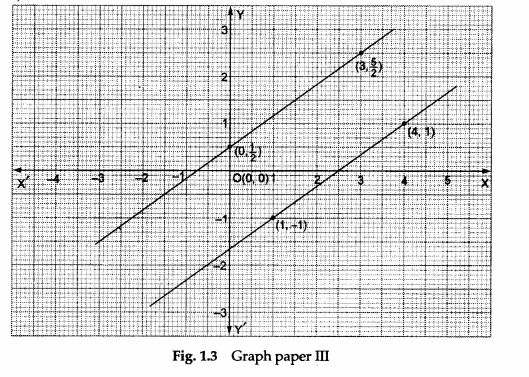
Observations
I. For the first system of equations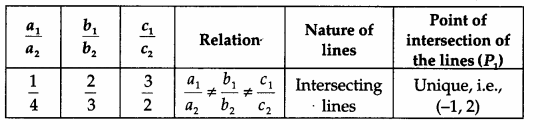
II. For the second system of equations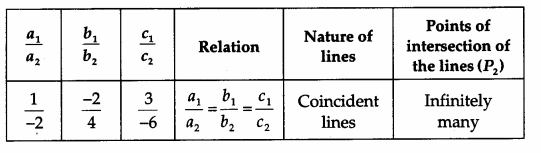
III. For the third system of equations
Conclusions
- The first system of equations is represented by intersecting lines, which shows that the system is consistent and has a unique solution, i.e., x = -1, y = 2 (see the first observation table).
- The second system of equations is represented by coincident lines, which shows that the system is consistent and has infinitely many solutions (see the second observation table).
- The third system of equations is represented by parallel lines, which shows that the system is inconsistent and has no solution (see the third observation table).
Remarks: The teacher must provide the students with additional problems for practice of each of the three types of systems of equations.

No comments:
Post a Comment