SEQUENCE:
A sequence is an arrangement of numbers in a definite order and according to some rule.
Example: 1, 3, 5,7,9, … is a sequence where each successive item is 2 greater than the preceding term and 1, 4, 9, 16, 25, … is a sequence where each term is the square of successive natural numbers.
TERMS :
The various numbers occurring in a sequence are called ‘terms’. Since the order of a sequence is fixed, therefore the terms are known by the position they occupy in the sequence.
Example: If the sequence is defined as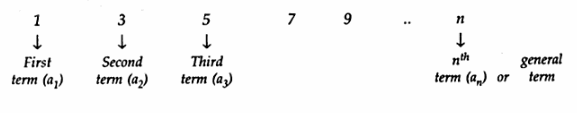
ARITHMETIC PROGRESSION (A.P.):
An Arithmetic progression is a special case of a sequence, where the difference between a term and its preceding term is always constant, known as common difference, i.e., d. The arithmetic progression is abbreviated as A.P.
Arithmetic Progression (AP)
Consider
(i) 1, 2, 3, 4, ……
(ii) 3, 3, 3, 3, …..
(i) and (ii) are the sequence of numbers, each number in these sequences is called a term.
An arithmetic progression (AP) is a sequence of numbers in which each term is obtained by adding a fixed number ‘d’ to the preceeding term, except the first term.
The fixed number is called the common difference. It can be positive, negative or zero.
Any Arithmetic progression can be represented as :
a, a + d, a + 2d, a + 3d,…..
where ‘a’ is the first term and ‘d’ is the common difference. Arithmetic progressions which does not have a last term are called Infinite Arithmetic Progression. e.g.:
6, 9, 12, 15,…….
Formula for common Difference (d)
A sequence of numbers a1, a2, a3…. is an AP if the difference a2 – a1, a3 – a2, a4 – a3…. gives the same value, i.e. if ak+1 – ak is the same for different values of k. The difference (ak+1 – ak) is called common difference (d). Here ak+1 and ak are the (k + 1)th and kth terms respectively.
∴ d = a2 – a1 = a3 – a2 = a4 – a3
nth Term (or General Term) of an Arithmetic Progressions
In an AP, with first term ‘a’ and common difference d, the nth term(or the general term) is given by,
an = a + (n – 1)d
Note that an AP can be finite or infinite according to as the number of terms are finite or infinite.
If there are m terms in an AP then am is the last term and is sometimes denoted by ‘l’.
Sum of the FIRST ‘n’ Terms of an A.P.
(i) The sum of the first n terms of an A.P. is given by![]()
where a is the first term and d is the common difference
(ii) If l is the last term of the finite A.P. say the nth term, then the sum of all terms of the A.P. is given by,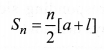
Note that sum of first n positive integers is given by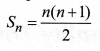
Arithmetic Mean Between Two Numbers
If a, b, c are in AP. Then b is called the arithmetic mean of a and c and is given by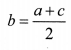

No comments:
Post a Comment