Ch-4: Quadratic Equations

 

Quadratic Equation

Standard form of the quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0.
Any equation of the form P(x) = 0, Where P(x) is a polynomial of degree 2, is a quadratic equation.

Zero(es)/Root(s) of Quadratic Equation

A real number α is said to be a root of the quadratic equation ax2 + bx + c = 0, a ≠ 0 if aα2 + bα + c = 0.
We can say that x = α, is a solution of the quadratic equation or that α satisfies the quadratic equation.
The zeroes of the quadratic polynomial ax2 + bx + c = 0 and the roots of the equation ax2 + bx + c = 0 are same. A quadratic equation has atmost two roots/zeroes.

Relation Between Zeroes and Co-efficient of a Quadratic Equation

If α and β are zeroes of the quadratic equation ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0 then

Methods of Solving Quadratic Equation

Following are the methods which are used to solve quadratic equations:

(i) Factorisation
(ii) Completing the square
(iii) Quadratic Formula

Methods of Factorisation

In this method we find the roots of a quadratic equation (ax2 + bx + c = 0) by factorising LHS it into two linear factors and equating each factor to zero, e.g.,
6x2 – x – 2 = 0
⇒ 6x2 + 3x – 4x – 2 = 0 …(i)
⇒ 3x (2x + 1) – 2(2x + 1) = 0
⇒ (3x — 2) (2x + 1) = 0
⇒ 3x – 2 = 0 or 2x + 1 = 0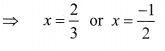

Necessary Condition : Product of 1st and last terms of eq. (i) should be equal to product of 2nd and 3rd terms of the same equation.

Method of Completing the Square

This is the method of converting L.H.S. of a quadratic equation which is not a perfect square into the sum or difference of a perfect square and a constant by adding and subtracting the suitable constant terms. E.g,
(1) x2 + 4x – 5 = 0
⇒ x2 + 2(2)(x) -5 = 0
⇒ x2 + 2(2)(x) + (2)2 – (2)2 – 5 = 0
⇒ (x + 2)2 – 4 – 5 = 0
⇒ (x + 2)2 – 9 = 0
⇒ x + 2 = ± 3
⇒ x = —5, 1
(2) 3x2 – 5x + 2 = 0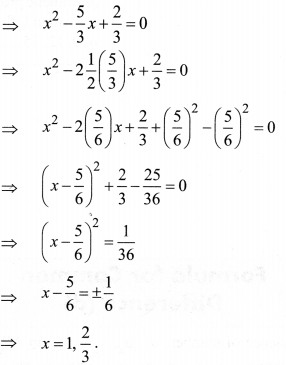

Quadratic Formula

Consider a quadratic equation: ax2 + bx + c = 0.
If b2 – 4ac ≥ 0, then the roots of the above equation are given by: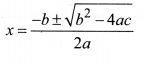

Nature of Roots

For quadratic equation ax² + bx + c = 0
(a ≠ 0), value of (b² – 4ac) is called discriminant of the equation and denoted as D.
D = b² – 4ac
Discriminant is very important in finding nature of the roots.
(i) If D = 0, then roots are real and equal.
(ii) If D > 0, then roots are real and unequal
(iii) If D < 0, then roots are not real.

Ch-5 Arithmatic Progressions

SEQUENCE:
A sequence is an arrangement of numbers in a definite order and according to some rule.
Example: 1, 3, 5,7,9, … is a sequence where each successive item is 2 greater than the preceding term and 1, 4, 9, 16, 25, … is a sequence where each term is the square of successive natural numbers.

TERMS :
The various numbers occurring in a sequence are called ‘terms’. Since the order of a sequence is fixed, therefore the terms are known by the position they occupy in the sequence.
Example: If the sequence is defined as

ARITHMETIC PROGRESSION (A.P.):

An Arithmetic progression is a special case of a sequence, where the difference between a term and its preceding term is always constant, known as common difference, i.e., d. The arithmetic progression is abbreviated as A.P.

Arithmetic Progression (AP)

Consider
(i) 1, 2, 3, 4, ……
(ii) 3, 3, 3, 3, …..
(i) and (ii) are the sequence of numbers, each number in these sequences is called a term.

An arithmetic progression (AP) is a sequence of numbers in which each term is obtained by adding a fixed number ‘d’ to the preceeding term, except the first term.
The fixed number is called the common difference. It can be positive, negative or zero.
Any Arithmetic progression can be represented as :
a, a + d, a + 2d, a + 3d,…..
where ‘a’ is the first term and ‘d’ is the common difference. Arithmetic progressions which does not have a last term are called Infinite Arithmetic Progression. e.g.:
6, 9, 12, 15,…….

Formula for common Difference (d)

A sequence of numbers a1, a2, a3…. is an AP if the difference a2 – a1, a3 – a2, a4 – a3…. gives the same value, i.e. if ak+1 – ak is the same for different values of k. The difference (ak+1 – ak) is called common difference (d). Here ak+1 and ak are the (k + 1)th and kth terms respectively.
∴ d = a2 – a1 = a3 – a2 = a4 – a3

nth Term (or General Term) of an Arithmetic Progressions

In an AP, with first term ‘a’ and common difference d, the nth term(or the general term) is given by,
an = a + (n – 1)d
Note that an AP can be finite or infinite according to as the number of terms are finite or infinite.
If there are m terms in an AP then am is the last term and is sometimes denoted by ‘l’.

Sum of the FIRST ‘n’ Terms of an A.P.

(i) The sum of the first n terms of an A.P. is given by

where a is the first term and d is the common difference
(ii) If l is the last term of the finite A.P. say the nth term, then the sum of all terms of the A.P. is given by,

Note that sum of first n positive integers is given by

Arithmetic Mean Between Two Numbers

If a, b, c are in AP. Then b is called the arithmetic mean of a and c and is given by

Areas of Sectors formed by vertices of a triangle

 

Areas of Sectors formed at the Vertices of a Triangle

Objective
To verify that sum of areas of three sectors of the same radii ‘r’ formed at the vertices of any triangle is          πr2 by paper cutting and pasting.

Prerequisite Knowledge

1. Concept of different types of triangles.
2. Definition of a sector.
3. Area of circle = πr2, r → radius.

Materials Required
Glazed paper, sketch pens, fevicol, a pair of scissors, pencil, geometry box.

Procedure

1. Draw three different types of triangles on a glazed paper as shown in fig. (i).
   (i) Equilateral ∆ABC
   (ii) Isosceles ∆PQR
   (iii) Scalene ∆XYZ
   
   
   
   
   
2. Cut an equilateral ∆ABC as shown in fig.(ii)
   
3. Taking vertices A, B and C as centres of ∆ABC, draw three sectors of same radii r.
   
4. Cut these three sectors and marked them as 1,2,3 and fill different colours.
   
5. Draw a straight line and mark any point ‘O’ on it. Place three sectors 1,2, 3 adjacent to each other so that the vertices A, B, C coincide with ‘O’ without leaving any gap as shown in fig. (v).
   
6. The same process (steps 1-5) can be taken up with isosceles triangle and scalene triangle fig. (i).

Observation

The shape formed on the straight line is a semi circle
∴ area of circle = πr2
∴ area of semicircle =  πr2

Result
It is verified that the sum of areas of three sectors of same radii ‘r’ formed at the vertices of any triangle is  πr2.

NCERT Class:10 ARITHMETIC PROGRESSIONS

SEQUENCE:
A sequence is an arrangement of numbers in a definite order and according to some rule.
Example: 1, 3, 5,7,9, … is a sequence where each successive item is 2 greater than the preceding term and 1, 4, 9, 16, 25, … is a sequence where each term is the square of successive natural numbers.

TERMS :
The various numbers occurring in a sequence are called ‘terms’. Since the order of a sequence is fixed, therefore the terms are known by the position they occupy in the sequence.
Example: If the sequence is defined as

ARITHMETIC PROGRESSION (A.P.):
An Arithmetic progression is a special case of a sequence, where the difference between a term and its preceding term is always constant, known as common difference, i.e., d. The arithmetic progression is abbreviated as A.P.

The general form of an A.P. is
∴ a, a + d, a + 2d,… For example, 1, 9, 11, 13.., Here the common difference is 2. Hence it is an A.P.

In an A.P. with first term a and common difference d, the nth term (or the general term) is given
by .
an = a + (n – 1)d.
…where [a = first term, d = common difference, n = term number
Example: To find seventh term put n = 7
∴ a7 = a + (7 – 1)d or a7 = a + 6d

Volume of a Cylinder

 

Volume of a Cylinder

Objective
To get the formula for the volume of a right circular cylinder in terms of its height and base radius experimentally.

Prerequisite Knowledge

1. Circumference of circle
2. Volume of cuboid

Materials Required
Plastic clay, cutter, thermocol.

Procedure

1. Make a cylinder of plastic clay of height say ‘h’ and base ‘A circle of radius r.
   
2. Cut the cylinder into 8 equal sectoral section with the help of cutter.
   
3. Place the sectoral segments alternatively to form a solid cuboid.
   

Observation

1. Combine cut out form a cuboid of height h and breadth r, i.e., height of cuboid = height of cylinder;
   breadth of cuboid = radius of cylinder.
2. The length of the cuboid =  of the circumference of base of cylinder.
3. Volume of cuboid = Volume of cylinder.
   V = l x b x h =  x 2πr x r x h = πr2h

Result
Thus the volume of cylinder is πr2h.

Tangents drawn from an External Point

 

 Tangents drawn from an External Point

Objective
To verify experimentally that lengths of tangents drawn from an external point to a circle are equal.

Tangent
A line touching the circle at a point is called a tangent to the circle.

Prerequisite Knowledge

1. Tangent to a circle.
2. Length of a tangent.
   

Materials Required
Glazed papers, a white chart paper, sketch pens, a pair of scissors, geometry box, fevicol.

Procedure

1. Cut a circle of any radius from a glazed paper and paste it on a white chart paper.
   
2. Take any point P on the circle.
   
3. From P, fold the paper in such a way that it just touches the circle at P. Press it and unfold to get a tangent PA.
   
4. From A, fold the paper to get tangent AQ.
   
5. Fold the circle along OA.
6. Join OP, OA, OQ.
   

Observation
Students observe that point P coincide with Q
∴ AP = AQ

Result
Thus it is verified that lengths of tangents drawn from an external point to a circle are equal.

Areas of Sectors formed at the Vertices of a Triangle

Areas of Sectors formed at the Vertices of a Triangle

Objective
To verify that sum of areas of three sectors of the same radii ‘r’ formed at the vertices of any triangle is          πr2 by paper cutting and pasting.

Prerequisite Knowledge

1. Concept of different types of triangles.
2. Definition of a sector.
3. Area of circle = πr2, r → radius.

Materials Required
Glazed paper, sketch pens, fevicol, a pair of scissors, pencil, geometry box.

Procedure

1. Draw three different types of triangles on a glazed paper as shown in fig. (i).
   (i) Equilateral ∆ABC
   (ii) Isosceles ∆PQR
   (iii) Scalene ∆XYZ
   
2. Cut an equilateral ∆ABC as shown in fig.(ii)
   
3. Taking vertices A, B and C as centres of ∆ABC, draw three sectors of same radii r.
   
4. Cut these three sectors and marked them as 1,2,3 and fill different colours.
   
5. Draw a straight line and mark any point ‘O’ on it. Place three sectors 1,2, 3 adjacent to each other so that the vertices A, B, C coincide with ‘O’ without leaving any gap as shown in fig. (v).
   
6. The same process (steps 1-5) can be taken up with isosceles triangle and scalene triangle fig. (i).

Observation
The shape formed on the straight line is a semi circle
∴ area of circle = πr2
∴ area of semicircle =  πr2

Result
It is verified that the sum of areas of three sectors of same radii ‘r’ formed at the vertices of any triangle is  πr2.

Area of Circle by Paper Cutting and Pasting Method

 

Area of Circle by Paper Cutting and Pasting Method

Objective
To obtain the formula for area of the circle i.e., πr2 by paper cutting and pasting method.

Prerequisite Knowledge

1. Definition of circle: A circle is the locus of a point in a plane which moves in such a way that its distance from a fixed point remains constant. Fixed point is known as centre and the fixed distance is known as radius of the circle.
   
2. Area of the circle: It is the measure of the region of the plane enclosed by it.
3. Circumference of the circle: Total length of its boundary.
   (C = 2πr, where ris radius of the circle)
   
4. Area of rectangle: length x breadth.
5. Sectors of a circle.
   

Materials Required
White paper, coloured sketch pen, a pair of scissors, fevicol, geometry box.

Procedure

1. Draw a circle of any radius on a sheet of paper (Take r = 6.5 cm) using compass
   
2. Fold it once along the diameter to obtain two semicircles as shown in fig. (ii).
   
3. Again fold the semicircle to get quarters of circle.
   
4. Repeat this process of folding upto four folds and then it looks like a small sector as shown in fig. (iv).
   
5. Press and unfold the circle. It is divided into 16 equal sectors.
   
6. Colour half of this circle i.e. 8 parts with one sectors with colour say blue and remaining 8 sectors different colour say orange.
   
7. Cut these sixteen different sectors of circle.
8. Cut one of the sector of orange colour into two equal parts as shown in the fig. (vii).
   
9. Arrange these seventeen sectors (one orange sector is divided in two parts) in alternate manner so that they form a rectangular shape as shown in fig. (viii).
   

Observation

1. Area of the rectangular shape so formed with seventeen sectors is same as the area of circle.
2. Length of the rectangular shape =  x circumference of circle =  x 2πr = πr.
3. Breadth of the rectangular shape = radius of circle
   ∴ Area of the rectangle = L x B = πr x r = πr2 sq. units.

Result
Area of a circle with radius r = πr2.